II. Description of Variables
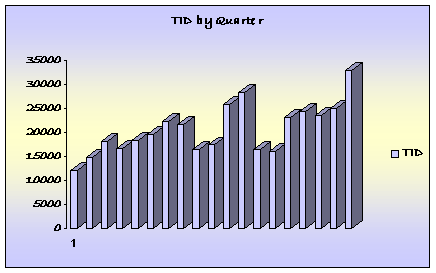
TID Variables
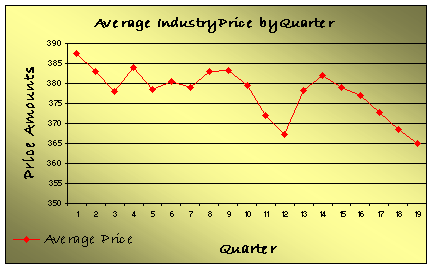
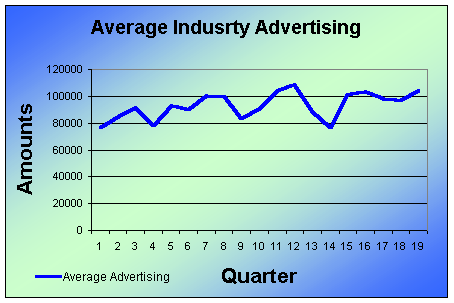
TID (Total Industry Demand) is used, along with (MS) Market Share to determine FD (Firm Demand). TID is calculated using independent variables, making TID a dependent variable. There are three independent variables that should be compared and studied to determine if they are relevant to the TID, and therefore can be used to estimate TID. First we looked at Quarter, then Average Industry Price of the product, and then Average Industry Advertising expenditure.
Summary data and charts were calculated to depict and explain these variables:
Quarter |
||||||||||||||||
|
|
|
|
||||||||||||||
|
Mean |
10 |
|
||||||||||||||
|
Median |
10 |
|
||||||||||||||
|
Standard
Deviation |
5.627314339 |
|
||||||||||||||
|
Minimum |
1 |
|
||||||||||||||
|
Maximum |
19 |
|
||||||||||||||
|
|
|
|||||||||||||||
|
Avg_Adv |
|
|
|
|
|
Mean |
93325.78947 |
|
Median |
93400 |
|
Standard
Deviation |
9828.045084 |
|
Minimum |
76800 |
|
Maximum |
108570 |
|
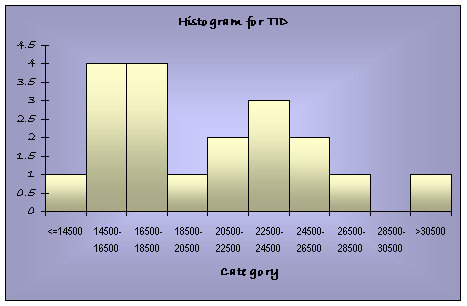
TID |
|
|
|
|
|
Mean |
20677.89474 |
|
Median |
19580 |
|
Standard
Deviation |
5233.005912 |
|
Minimum |
12020 |
|
Maximum |
32850 |
|
|
|
From these graphs and summary data, much information can be obtained. By graphing the variables versus time (Quarter); trends in the TID, Average price, and Average advertising expenditure appear. From the summary data of the TID, we show that the mean is 20678, and the Standard deviation is 5233. From this we can predict that if our estimate of the TID falls between 1 standard deviation from the mean (difference of 5233), we can be 68% sure that out estimate is correct. The same assumption can be made using the Standard Deviations and Means of the other variables.
Next, we were concerned about whether the independent variables have a relationship to the dependent variable or not. There needs to be a relationship in order to correctly add the independent variables to the model to estimate the TID, which is the dependent variable. In order to determine a relationship, a correlation analysis needs to be performed:
|
|
TID |
Quarter |
Avg_Price |
Avg_Adv |
|
TID |
1 |
|
|
|
|
Quarter |
0.694657 |
1 |
|
|
|
Avg_Price |
-0.88869 |
-0.703 |
1 |
|
|
Avg_Adv |
0.882219 |
0.522361 |
-0.74883 |
1 |
In the correlation matrix, there needs to be a high correlation between the dependent variable and the independent variables (either negative or positive). We show that there is a high correlation between TID and all the independent variables. There also needs to be a low correlation between the independent variables for there to be a definite correlation between the respective independent variable and the dependent variable. There are high correlations between the independent variables, as highlighted in yellow. Since there is a high correlation, one needs to refer to the p-value to best determine the relationship between the independent variables and the dependent variables. (See model section below).
You can also look at the scatter plots to determine relationships:
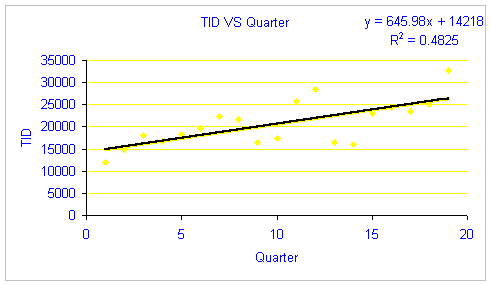
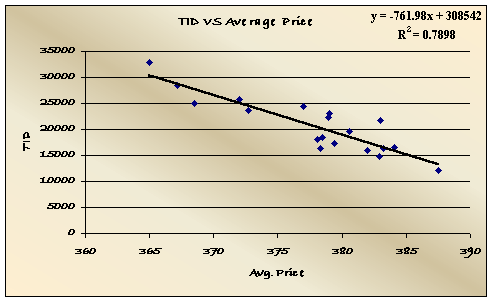
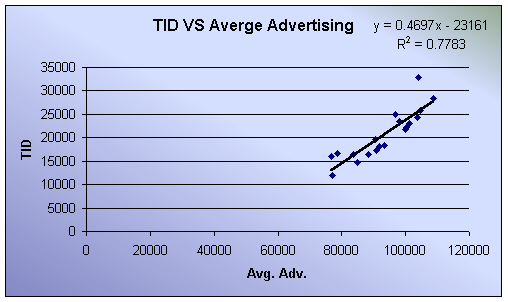
The scatter plots show relationships and trends, as well as display the equations used to estimate the dependent variables and R-Square. The higher the R-squared the better. The R-squared between TID and Quarter is low, so there needs to be more test done to determine if there is high relationship between the TID and Quarter. (This test can be seen in Section III of this report).